Seguimos analizando los métodos de integración, y esta vez toca el turno a la técnica de integración mediante fracciones parciales. Así que sin más preámbulos, te invito a que analices muy bien la siguiente información que te servirá de introducción al tema que abordarás más adelante.

El método de fracciones parciales utilizado en el cálculo integral consiste en tomar un cociente de polinomios difícil de calcular para convertirlo en fracciones más simples, que al resolverlas permitan obtener una integral mas sencilla de resolver de una manera inmediata. Este método se puede utilizar siempre y cuando la función cumpla con un requisito muy importante, el cual consiste en que el grado del polinomio del denominador sea obligatoriamente mayor que el grado del numerador.
Podemos representar una integral por fracciones parciales mediante la siguiente forma:
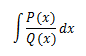
Donde:
- P(x) y Q(x) son polinomios
- El grado de Q(x) es mayor que el de P(x)
Hay dos puntos muy importantes que se necesitan resaltar a partir de la información presentada:
- Las fracciones parciales se utilizan como apoyo para descomponer expresiones racionales complicadas y transformarlas en sumas de expresiones más sencillas.
- La fracción parcial se utiliza en el álgebra para reducir los grados del numerador o el denominador de una función racional y el resultado que se obtiene de la extensión parcial de la fracción expresa dicha función como la suma de las fracciones donde:
- El denominador de cada fracción es imposible de factorizar y,
- El numerador es un polinomio de grado más pequeño que el denominador no factorizable.

