Hola y bienvenido a tu blog de matemáticas discretas. Durante esta sesión practicaremos mucho de lo que aprendimos anteriormente en la sesión dedicada al conocimiento del sistema de numeración octal.
Ahora, nos queda claro que la parte importante del sistema octal es su base ocho y en las ventajas que representa para con los sistemas informáticos y la electrónica digital así como la facilidad de conversión entre sistemas numéricos binarios y octales, su relación con las unidades de almacenamiento en disco duro y demás.
Sin embargo esto no es todo lo que la base 8 ha logrado por la informática. De hecho hay un área en la que poco se sabe del número ocho pero juega un papel importante y si te gustan los video juegos o películas animadas por computadora es casi seguro que lo hayas visto alguna vez sin notarlo.
Me refiero a una herramienta de diseño y creación de gráficos tridimensional conocida como Octree, este nombre viene dado a partir de la palabra oct (octante) y tree (árbol).
Un octree es una estructura en “árbol” de datos en la cual cada nodo interno tiene exactamente 8 “hijos”. Las estructuras octree se usan mayormente para particionar un espacio tridimensional, dividiéndolo recursivamente en ocho octantes.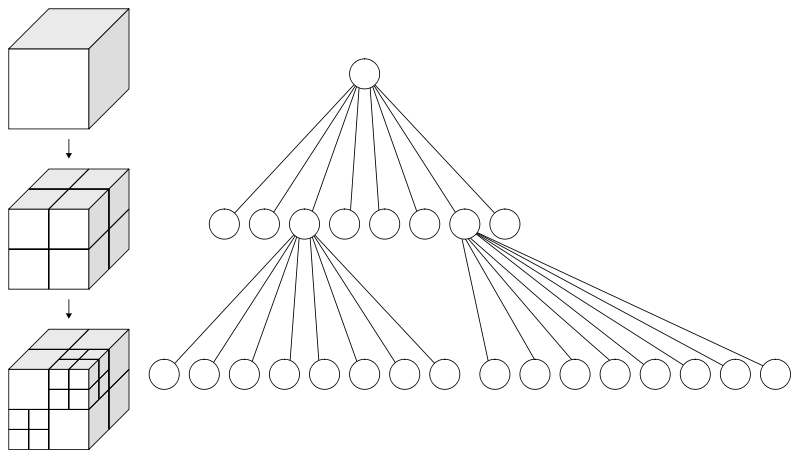
Esto se logra dividiendo a un cubo imaginario. Las estructuras octree se usan mayormente para particionar un espacio tridimensional, dividiéndolo recursivamente en ocho octantes, es por esto que este método es probablemente el más adecuado cuando se quiere representar por gráficos generados por computadora a las figuras geométricas flotando en el “espacio” como por ejemplo una animación del sistema solar.
Por otro lado El algoritmo de cuantización del color inventando por Gervautz y Purgathofer en 1988 codifican los datos de color de una imagen como un octree con hasta nueve niveles de profundidad. Las estructuras octree son usadas ya que 23 = 8 y también hay tres componentes de colores para el sistema de color RGB.
El algoritmo es de una memoria altamente eficiente ya que el tamaño del árbol se puede limitar. El nivel del fondo del octree consiste de nodos hojas que acumulan datos de color que no están representados en el árbol; estos nodos contienen inicialmente bits simples. Si en ingresan en el octree muchos más números de colores de paletas que los deseados, su tamaño se puede reducir continuamente buscando un nodo de nivel bajo y promediando sus datos de bit hasta en un nodo hoja, podando parte del árbol. Una vez que el muestreo está completo, al explorar todas las rutas en el árbol hasta las hojas nodos, y al tomar nota de los bits a lo largo del camino, se obtendrá aproximadamente los números de colores requeridos.
Finalmente existen los llamados motores gráficos, que son un conjunto de funciones, librerías, herramientas y demás que permiten la programación y “dibujado” de escenarios y objetos en tres dimensiones. Muchos de estos se valen de estructuras del tipo octree para realizar muchas de sus funciones.


0 Comentarios