Supóngase dada una cantidad finita de números, digamos ![]() y consideramos su suma.
y consideramos su suma.
![]()
En ocasiones es conveniente más hacer breve esta expresión, y esto se logra mediante el símbolo de suma ![]() , llamado sumatoria, cuya utilización pasamos a describir.
, llamado sumatoria, cuya utilización pasamos a describir.
Pondremos:
![]()
En el especial caso en que sea ![]() ,
,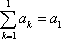 .
.
El elemento ![]() se llama término general de la suma y, en muchos casos prácticos, es preciso conocer el aspecto de este término general.
se llama término general de la suma y, en muchos casos prácticos, es preciso conocer el aspecto de este término general.
El número ![]() que figura debajo del símbolo
que figura debajo del símbolo ![]() se llama índice de sumatoria, y entendemos que los valores que toma este índice son
se llama índice de sumatoria, y entendemos que los valores que toma este índice son ![]() .
.
Más generalmente, si ![]() y
y ![]() son dos números enteros, con
son dos números enteros, con 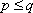 , pondremos
, pondremos
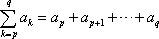
En este contexto, el número 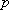 se llama límite inferior de la suma, en tanto
se llama límite inferior de la suma, en tanto 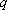 es el límite superior de esa suma.
es el límite superior de esa suma.
Ejemplos.
a) Se quiere expresar la suma de los cuadrados de los primeros 10 naturales:
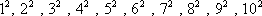
Es decir:
![]()
Como es fácil ver, el término general es 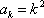 , con lo que nuestra suma puede adquirir el aspecto más descansado
, con lo que nuestra suma puede adquirir el aspecto más descansado 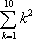 . Así, se tiene la igualdad
. Así, se tiene la igualdad
![]()
Donde el lado izquierdo debe entenderse como una notación más compacta del lado derecho.
Si queremos considerar solamente 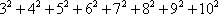
pondremos
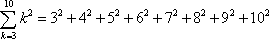
b) La suma 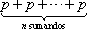 , con la notación de sumatoria, se escribe
, con la notación de sumatoria, se escribe 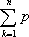 , lo cual no nos debiera sorprender durante demasiado tiempo. La apariencia anómala se debe a que no figura algo así como
, lo cual no nos debiera sorprender durante demasiado tiempo. La apariencia anómala se debe a que no figura algo así como 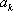 , cosa que se subsanaría formalmente definiendo
, cosa que se subsanaría formalmente definiendo  . Claramente esta precisión sería tediosa y absolutamente inútil.
. Claramente esta precisión sería tediosa y absolutamente inútil.
Con esta notación 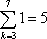 ya que estamos sumando el número a medida que avanza el índice de sumación:
ya que estamos sumando el número a medida que avanza el índice de sumación: 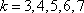 habiendo entonces
habiendo entonces 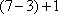 sumandos. Por lo mismo, el lector entenderá las igualdades
sumandos. Por lo mismo, el lector entenderá las igualdades 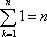 y
y 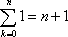 .
.
c) Fijemos un número real  , y consideremos sus primeras potencias
, y consideremos sus primeras potencias
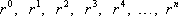
Utilizando la notación estándar para su suma, se tiene
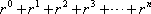 .
.
Con la notación compacta, y teniendo presente que el término general es 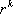 , ponemos
, ponemos
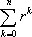
Así
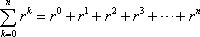
Como 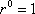 y
y 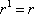 , será más natural poner
, será más natural poner
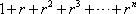


0 Comentarios